Complexity

Prev: dynamic-programming-part-4-rods-subsetsums-pseudopolynomial Next: course-review

Decision Problems

Decision problems are problems that can be solved with a “yes” or “no” answer.

Some problems might include negative cycle (does a provided graph G contain a negative cycle in it?)

Programs are decidable if there exists a program to solve the problem in finite time.

Decidability

Not all problems are solvable, actually.

Assume that a program is a finite string of bits from the set $\{0,1\}$ with a finite length, n. Assume that a problem is an ininite string of bits from the set $\{0,1\}$.

The number of programs is in $\mathbb{N}$, which is countably infinite. The number of problems is in $\mathbb{R}$, which is uncountably infinite.

We know that $\mathbb{N}$ $\ll$ $\mathbb{R}$, so most decision problems must not be solvable by any program.

Some problems, like the halting problem (or to determine any characteristic of a program in finite time for all programs) are undecidable.

Another way to think about it is if you had infinite bits ($\mathbb{N}$), would you be able to express all the real numbers in (0..1) ($\mathbb{R}$)?. The answer is no, because you lack enough entropy to do so ($\mathbb{R}$) would have a base of infinity, whereas N would have a base of 2 in this case).

Decidable Decision Problems

There are a few main classes of decision problems:

• $\mathbb{R}$: problems decidable in finite time ($\mathbb{R}$ stands for recursive)
• $EXP$: problems decidable in exponential time $2^n$
• $P$: problems decidable in polynomial time $n^c$

These sets are distinct, so $P$ is strictly smaller than $EXP$, and $EXP$ is strictly smaller than $\mathbb{R}$.

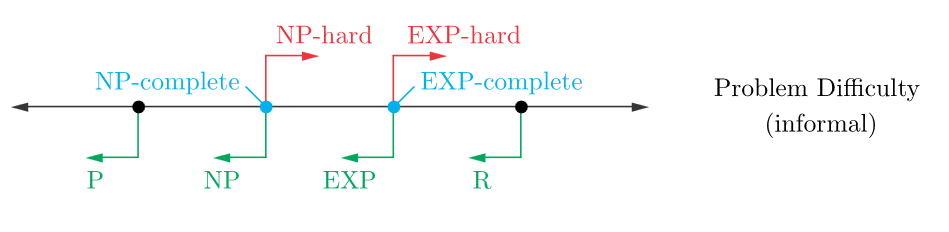
Nondeterministic Polynomial Time (NP)

$P$ is the set of decision problems for which there is an algorithm A that for every input of size N runs in polynomial time and solves it correctly.

$NP$ is the set of decision problems for which there is a verification algorithm V that takes as input I, and a certificate bit string of length polynomial to the size of I that verifies that the certificate is either valid or not to solve the problem.

The biggest open question in theoretical computer science is whether or not $P=NP$, and/or $NP=EXP$.

Most people think no, because generating solutions is harder than checking, and since NP algorithms require luck to be solvable in P time, it would be odd to postulate that luck has no value (if you won the lottery every time you bought a ticket vs winning the lottery at a normal cadence, some 1 in 1 million times), are these the same?

Reductions

• To solve a problem A that you don’t know how to solve, but you know how to solve B, try to convert A into B.
• Then solve B.
• If B can be used to solve A, B is at least as hard as A. (A $\ll$ B).
• Any problem that is at least as hard as NP is called NP-Hard.
• Any problem that is in NP and NP-Hard is called NP-Complete.
• All NP-Complete problems are reducible to each other.

NP-Complete Problems

• Boolean satisifiability (given n booleans, can you use and and or operations to set the equation to true?).
• 3-Partition (given n integers, divide them into three sets with equal sum) is NP-Complete
• Longest common subsequence of n strings (where n is not polynomially bound) (if n is a polynomial, it is in P).
• Longest simple path in a graph (only visiting each node once).
• Traveling Salesman Problem (shortest path that visits all vertices of a given graph
• Shortest path amidst obstacles in 3D (in 2D it is polynomial).
• 3-coloring a graph (2-coloring is in $P$)
• Clique problem (finding all groups of nodes who are connected to each other).
• Set packing (for a set of subsets S, are there any such subsets with length K in which none of them share an element?)
• Set covering (given a set of elements $\{1,2,...n\}$, and a set of m sets, find the smallest union which contains the universe).
• Partition (for a given set S of positive integers, can it be partitioned into two sets (A, B) such that the sum of numbers in A equals the sum of the numbers in B?) There is a DP psuedo-poly time algorithm for this.
• Job Scheduling (given a set of tasks T, and a set of machines M, find a schedule which maximially uses all the machines to do the work in the shortest time possible).

Prev: dynamic-programming-part-4-rods-subsetsums-pseudopolynomial Next: course-review