62-unique-paths

Unique Paths

Unique Paths

At first this question seems simple, you can just recursively dfs through and guide the robot from start to end:

I tried this, and got Time Limit Exceeded, because this is an exponential time algorithm :(.

We need to improve our approach, because we’re calculating the same paths over and over again, which is wasteful work. The intuition here is that it there are as many paths to the bottom right (m - 1, n - 1 in the matrix) as there paths from your neighbor to the right + paths from your neighbor below you.

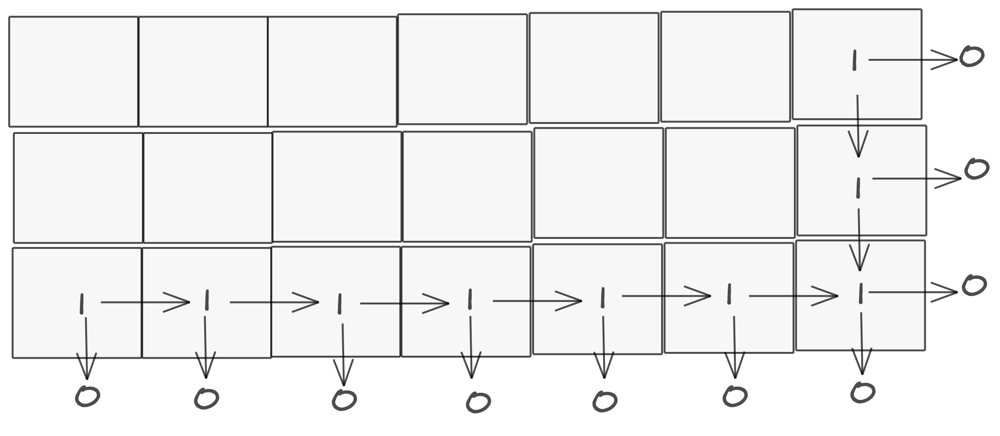
Imagine that there’s an imaginary row of 0s at row m and col n, and with there being 1 path to get to bottom right in the square at bottom right, you calculate the weights of the bottom row and the rightmost column by having each square ask its neighbor to the right and its neighbor below it how many paths there are, and add them up.

With this approach, there is exactly 1 way to get to the bottom right square if you’re on the bottom right square.

If you are on the rightmost column of the matrix, there is exactly 1 way to the bottom right, because you can only go down. (1 + 0 for all cols)

If you are on the bottommost row of the matrix, there is exactly 1 way to the bottom right, because you can only go right. (0 + 1 for all rows)

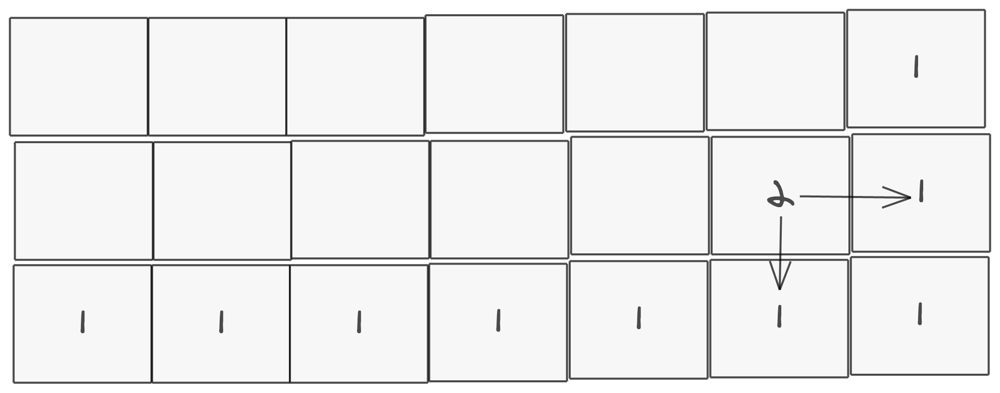
Now, we continue doing this for the row above the bottommost row, the column to the left of the rightmost column.

The right neighbor has a weight of 1, and the bottom neighbor has a weight of 1, which means this neighbor should have a weight of (1 + 1) or 2.

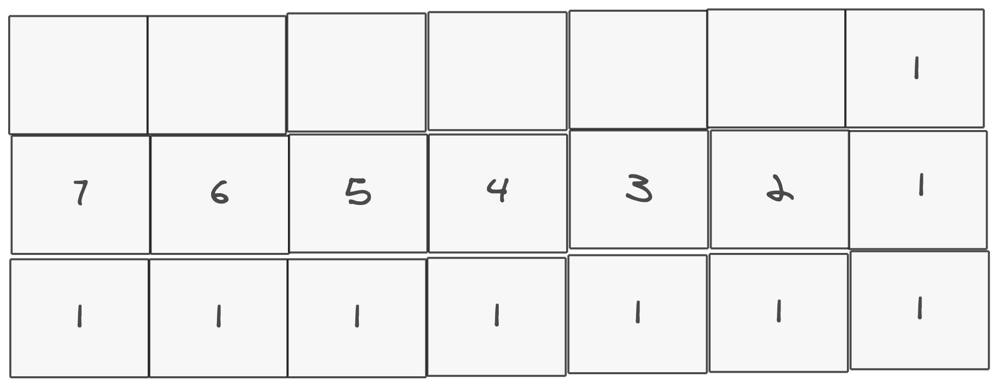
We can calculate the rest of the row like so using the same logic:

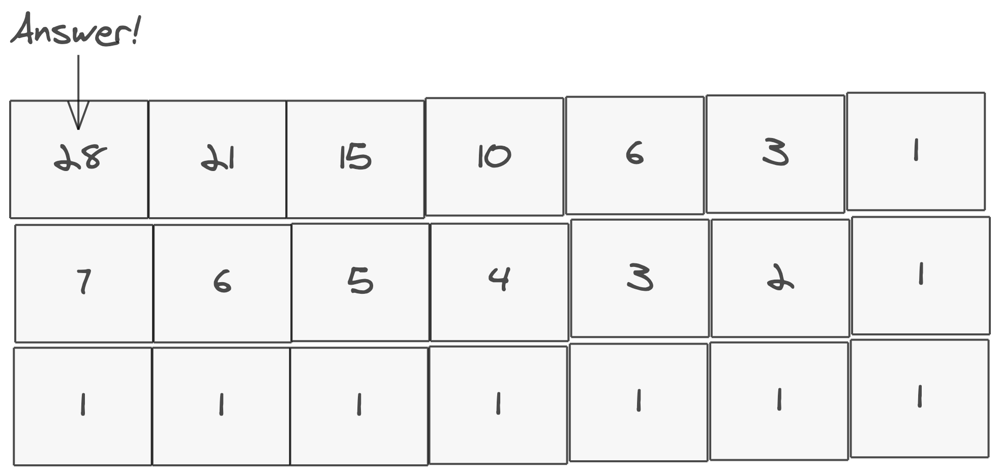
And then the first row to get a total of 28 paths to the bottom right.

Now for the translation in code, we could do the same thing, but we would have to iterate through the matrix in reverse, which is a bit confusing.

I decided to do it right side up, so the code does the same thing as above, just upside down.

The answer is in the matrix at [m-1][n-1] instead of [0][0] this way, which allows us to calculate our own weight by asking the neighbors at [i-1][j] + [i][j-1].

First, i iterated through the numbers to create the matrix of size m * n. Then, i iterated through it again to fill the matrix with 1 if its i == 0 or j == 0. Lastly, i iterated through it again to calculate the current weight, by having each [i][j] in the matrix equal [i-1][j] + [i][j-1]. This leads the answer to be at [m-1][n-1] instead of at [0][0], but is the same idea.

{{# include _include/code/algorithms/leetcode/explanations/62-unique-paths/main.py }}